Skip to main content

Einführung

Bildmatrix​

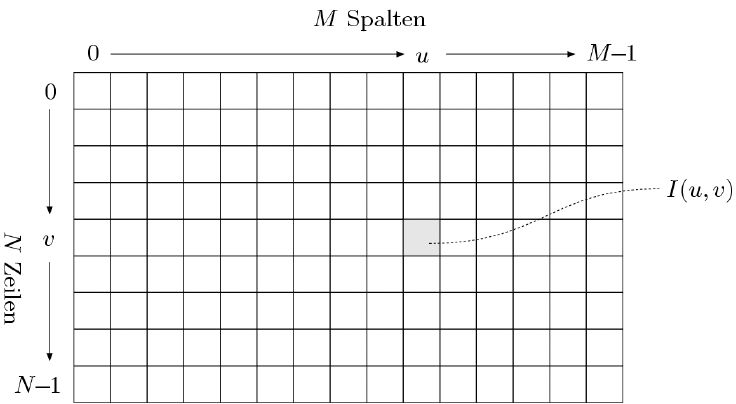
Wir wissen das ein Bild eine Breite und eine Höhe und aus mehreren Pixel besteht. Dabei hat jeder Pixel(oft auch Bildwert) einen Intensitätswert. Je nach Bildtyp repräsentiert dieser Intensitätswert etwas anderes. Wir können uns also im allgemeinen ein Bild als eine mathematisch Funktion vorstellen.

I:N×N↦PI:\mathbb{N}\times\mathbb{N} \mapsto P

Dabei sind die zwei natürlichen Zahlen die Koordinaten des Pixels auf x-Achse (Breite) und auf der y-Achse (Höhe) und der Wert der heraus kommt PP entspricht dem Intensitätswert des Pixels.

Wir können dann ein Bild in einer Matrix darstellen mit der Breite MM und die Höhe NN in Anzahl Pixel/Bildwerte. bildMatrix

Bildvektor​

Das ganze Bild wird in einem Vektor/Zeilenvektor abgespeichert mit der Länge M⋅NM \cdot N. Der Vorteil dabei gegenüber einer 2D Matrix ist, dass der Zugriff effizienter und einfacher ist.

Problematik???

Bildtypen​

Binärbild​

Ein Binärbild hat nur zwei mögliche Werte, weiss oder schwarz welches 1 und welches 0 ist, ist nicht immer klar.

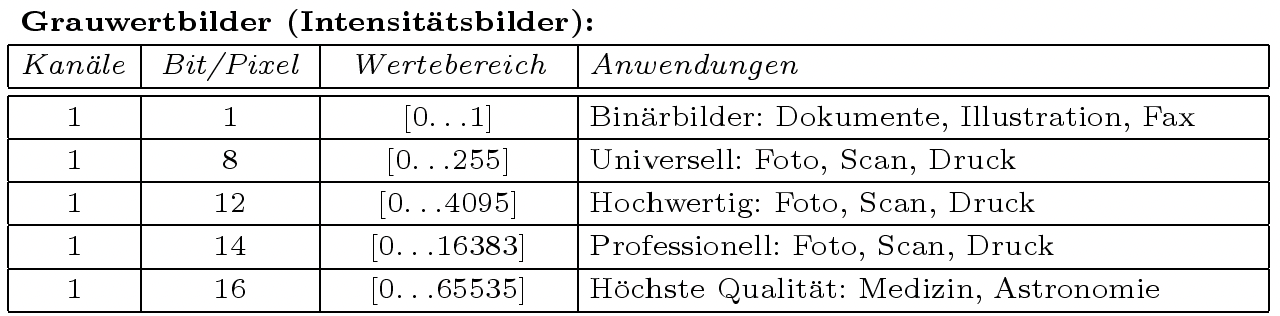
Grauwertbild/Intensitätsbild​

Ein Grauwertbild hat nur ein Kanal, der die Helligkeit, Intensität oder Dichte beschreibt. wertebereichGrauwertBild

Farbbild​

Wahl eines Farbraums z.B RGB, RGBA oder CYKA.

Vollfarbenbild​

Indexbild​

Bildformate​

Ohne kompression​

Mit verlustloser Kompression​

Mit verlustbehafteter Kompression​

Mit verlustloser/verlustbehafteter Kompression​

Wertbereiche​

Umrechnungen​

Region of Interest - ROI​

Farbbild zu Grauwertbild​

Grauwertbild zu Binärbild - Dithering​